La rifrazione della luce

Presentiamo un brano del grande storico dell'astronomia e della fisica antica, il danese Olaf Pedersen, tratto dal suo bellissimo libro di testo “Early Physics and Astronomy” (1993).

Gli specchi ustori di metallo lucidato erano ben noti nell'Antichità, e già a partire dal V secolo a.C. i  Greci avevano una certa conoscenza pratica della rifrazione della luce, e sapevano come costruire vetri ustori (lenti). Ma il fenomeno non fu studiato accuratamente prima di Tolomeo, che ne fornì una descrizione magistrale nella sua Ottica.
Per prima cosa cita un “esperimento dimostrativo” fatto con un baptistir (v. figura), che è una specie di ciotola. Se, dice, si guarda da A poco oltre il bordo in B, una moneta in G sarà invisibile. Ma se la ciotola è riempita con acqua la moneta sembra essere sollevata in una posizione superiore, dalla quale si può vedere. Tolomeo postula che il luogo apparente della moneta è il punto K in cui si intersecano la verticale passante per G e quella prolungata del raggio AB.
 

 

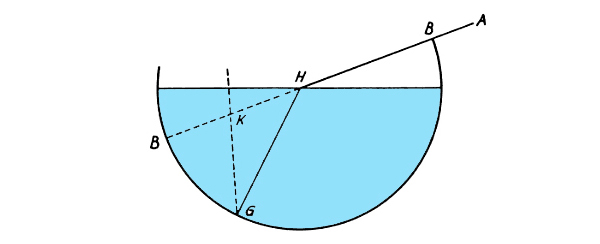
Dopo questa dimostrazione introduttiva Tolomeo proseguì con un esperimento quantitativo, utilizzando il disco di rame graduato o goniometro del suo esperimento sulla riflessione. Il disco è ora collocato in posizione verticale all'interno di un vaso riempito di acqua fino al livello del diametro DB (v. figura).
 

 

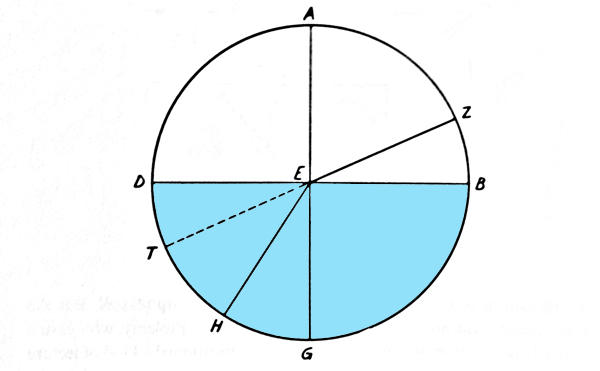
Il centro E e un punto Z sono indicati da piccoli segni colorati. Sotto la superficie viene spostato un puntatore lungo la circonferenza finché non è visto in H, sulla continuazione del raggio incidente ZE. L'angolo di incidenza AEZ = i e l'angolo di rifrazione HEG = r possono essere letti sullo strumento.

Misurazioni di questo tipo sono realizzate con raggi che passano dal vetro all'aria (sempre secondo l'assunto che i raggi provengano dall'occhio). In questo caso un semicilindro di vetro viene fissato alla metà inferiore del disco di rame, e le posizioni dell'occhio e del segno Z sono invertite. Infine, Tolomeo studiò le rifrazioni dal vetro all'acqua. I suoi risultati sono stati riportati nella forma di tabelle frequentemente citate nei testi di ottica fino alla scoperta della legge di rifrazione esatta nel XVII secolo.



 

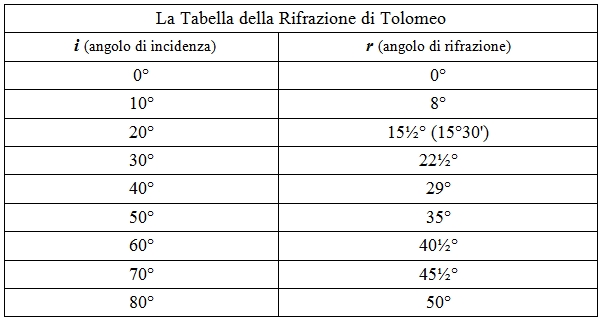
Né nell’Antichità né nel Medioevo gli scienziati riuscirono a raccogliere i risultati in una relazione matematica di esattezza soddisfacente. A volte è stato utilizzata la formula i / r = costante, che, tuttavia, dà solo un'espressione molto approssimativa dei valori trovati. Sembra che Tolomeo stesso preferisse una relazione corrispondente a quello che si potrebbe oggi esprimere con la formula r = ai - bi² che, con valori adeguati di a e b, fornisce un'approssimazione migliore.

Rifrazione Atmosferica

I Greci furono il popolo che scoprì la rifrazione della luce nell'atmosfera. In Sul moto circolare dei corpi celesti  Cleomede (le cui date sono incerte, probabilmente I sec d.C.) racconta di aver osservato un'eclisse di Luna prima del tramonto. Dapprima non poteva spiegare il fenomeno, perché una tale eclisse presuppone che Sole, Terra e Luna siano allineate, in modo che il Sole e la Luna, visti dalla Terra, debbano essere diametralmente opposti nel cielo, e non dovrebbe essere possibile quindi riuscire a vedere il Sole e al tempo stesso la Luna eclissata.

Cleomede allora avanzò l'ipotesi che i raggi del Sole non passassero attraverso l'atmosfera della Terra in linea dritta (vedi figura). Se si assume che essi si pieghino verso la Terra, i dischi di Sole e Luna saranno entrambi apparentemente sollevati sopra l'orizzonte, e il fenomeno è spiegato. Cleomede mostra che una tale spiegazione è ragionevole per mezzo dell'esperimento sopra discusso: se una monetina viene posta in una bacinella, nascosta sotto il bordo quando l'occhio è in una certa posizione, diventa visibile quando l'acqua è versata nella bacinella. Ossia, l'immagine della monetina è sollevata dall'acqua nello stesso modo in cui il Sole e la Luna sono apparentemente sollevati dall'atmosfera.
 

 

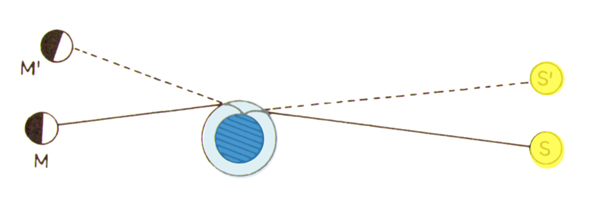
Talete di Mileto
c. 625 a.C.  a  c. 545 a.C.

È il primo dei filosofi naturali ionici, forse di origine fenicia. Talete viaggiò in Egitto e dopo il suo ritorno a Mileto divenne il disseminatore delle conoscenze di matematica egizia tra i greci. Nella filosofia naturale ha preparato la strada per una descrizione razionale dei fenomeni discostandosi dalla concezione mitologica della natura, cercando invece di spiegare l'evoluzione dell'universo a partire da una materia prima (l’acqua), da cui emergono tutte le altre sostanze. I suoi scritti sono andati perduti e l'effetto del suo contributo alla scienza è piuttosto incerto.

Cleomede
Probabilmente del primo secolo d. C.

Un astronomo stoico, di difficile datazione. Autore di un trattato Il motu circulari corporum caelestium (testo greco con traduzione latina di H. Ziegler, Leipzig, 1891, trad tedesca A. Czwalina Die Kreisbewegung det Gestirne, Leipzig, 1927 (Ostwalds Klassiker N° 220); Trad. francese R. Goulet, Cléomede: Théorie élémentaire, Parigi, 1980), in gran parte basato su Poseidonio, ma contenente anche contributi originali all'ottica, per esempio la scoperta della rifrazione atmosferica.

Tolomeo
circa 100-165  D.C.

Claudio Tolomeo (da Tolemaide in Egitto) ha trascorso quasi tutta la sua vita ad Alessandria lavorando su dimostrazioni in tutte le principali branche della matematica applicata. Egli è più attento di altri autori antichi nel riferire le sue fonti ed è, per questo motivo, spesso stato considerato come un mero compilatore. In realtà, egli fu uno dei più dotati fra gli scienziati ellenistici, e ha dato contributi originali di astronomia, fisica e matematica, che hanno evidenziato una chiara visione delle relazioni tra esperienza, ipotesi e teorie. L'impatto del suo lavoro è stato avvertito fino al XVII secolo, in particolare in astronomia, dove ha creato il quadro teorico utilizzato fino al tempo di Keplero.
Il suo lavoro principale è stato la "Grande Collezione", o "Grande Trattato", meglio conosciuto come Almagesto, in cui ha continuato l'opera di Ipparco e Apollonio con le sue teorie geometriche del moto dei pianeti (ed. JL Heiberg et al . 2 voll, Leipzig, 1898-1903;. Traduzione in inglese di GJ Toomer Almagesto di Tolomeo, London, 1984 (ottime note); in francese a cura di N. B. Halma 2 voll, Parigi 1816 (ristampa 1927); in tedesco a cura di M. Manitius, 2 voll, Leipzig, 1912 - 1913 (ristampa 1963)).
Un certo numero di Opere astronomiche minori (ed. JL Heiberg et Ludwig Nix, Leipzig, 1907) contiengono tra gli altri trattati una parte delle “Ipotesi” che descrivono le sue idee fisiche dell'universo e il calcolo della sua dimensione, un'altra parte dello stesso lavoro è stata scoperta e pubblicata da una versione araba (B. R  Goldstein "Versione araba delle Ipotesi del Planetario di Tolomeo" (con traduzione inglese.), Trans. Amer. Philos. Soc., VII (1967)).
Il suo Tetrabiblos o Liber Quadripartitum (edizione con traduzione inglese a cura di  F. E Robbins, Londra (Loeb), 1940) è una esposizione sistematica di astrologia. Tra le sue opere minori si trova il testo Analemma, che tratta di proiezione parallela della sfera celeste, fornendo la teoria fondamentale delle meridiane. Un altro suo testo è il Planisphaerium sulla proiezione stereografica che dà la teoria matematica sottostante l'astrolabio (traduzione in tedesco a cura di J. Drecker, Isis, IX, (1927), 255-278).
Le "Tavole Manuali", o Tabulae manuales, con le loro Canones, si trovano in una versione di Teone di Alessandria (edizione e traduzione a cura di N. B Halma, Commentaire de Théon d’Alexandria sur les tables manuelles de Ptolémée. I, Parigi, 1822) e sono una versione riveduta delle tabelle dell'Almagesto con intervalli più piccoli degli argomenti.
La grande Geografia  della massima importanza per la nostra conoscenza del mondo antico, e per la storia della cartografia (testo greco con traduzione francese a cura di N. B. Halma, Parigi, 1828; traduzione in Inglese a cura di E. L. Stevenson, New York, 1932. Una edizione in latino Seb Muster, Basilea, 1540,  stata ristampata in facsimile da R. A. Skelton, Amsterdam, 1966. Una edizione del Codex Urbinas Graecus LXXXII da J. Fischer. Claudii Ptolemaei Geographiae, Leiden - Lipsia 1932 ,  dotata di un ottima introduzione biografica).
L'Ottica di Tolomeo sopravvisse solo in una traduzione araba che nel XII secolo fu tradotta in latino da Eugenio di Palermo (a cura di A. Lejeune, L' optique de Claude Ptolomee, Lovanio, 1956). Tra i suoi altri scritti si trovano libri sulla teoria della musica, e su problemi filosofici, questi ultimi rivelano Tolomeo come un aristotelico fortemente influenzato dalle idee stoiche.

Ibn al-Haitham
di Bassora - c. 965 - 1039

In latino Alhazen, il più grande fisico dei musulmani, Ibn al-Haitham produsse il suo miglior lavoro in Egitto sotto al-Hakim (966 -1020). Il suo più importante risultato si occupa di specchi sferici, della rifrazione della luce, che viene esaminata sperimentalmente, e di altri argomenti ottici. Il suo Ottica (edizione Baarmann, Abhandlung über das Licht von Ibn al-Haitham, testo arabo con traduzione in tedesco Zts Deuts Morgenl Ges, XXXVI, (1882), 195-237; la più vecchia traduzione in latino edizione Risner, Alhazeni Opticae Thesaurus, Basilea 1572, unitamente allfOttica di Witelo, ristampato New York, 1972) costituisce un punto di partenza per Witelo ed era ancora importante nel XVI secolo. Come astronomo, Alhazen fu molto critico verso Aristotele, sottolineando la necessità di una astronomia "fisica" delle sfere materiali.